The Pennsylvania State University, Spring 2021 Stat 415-001, Hyebin Song

Interval Estimation

Go to course main page

Introduction to Interval Estimation

Learning objectives

• Understand the concepts of interval estimators, confidence coefficients, and and interval estimates
• Understand how to construct and interpret $1-\alpha$ confidence intervals.

Interval estimators and interval estimates

• Definitions

  • Interval estimator for $\theta$: a random interval $[l(X_1,\dots,X_n),u(X_1,\dots,X_n)]$ such that $l(X_1,\dots,X_n)\leq u(X_1,\dots,X_n)$, which is designed to infer a specific parameter $\theta$.

    • We construct $l(\cdot)$ and $u(\cdot)$ so that an interval estimator $[l(X_1,\dots,X_n),u(X_1,\dots,X_n)]$ contains $\theta$ at least $100(1-\alpha)$% times. In other words,
  $$P_\theta(l(X_1,\dots,X_n)\leq \theta \leq u(X_1,\dots,X_n)) \geq 1-\alpha$$

  • This $1-\alpha$ is called the confidence coefficient .

  • Interval estimate for $\theta$: an observed interval $[l(x_1,\dots,x_n),u(x_1,\dots,x_n)]$.

    • If the corresponding interval estimator has the confidence coefficient of $1-\alpha$, the interval estimate of $\theta$ is also called as a $100(1-\alpha)$% confidence interval for $\theta$.

• Remark

  • The probability that a 95% confidence interval (a fixed interval) contains the parameter $\theta$ is $1$ (parameter is in the interval) or $0$ (parameter is not in the interval). If we construct many 95% confidence intervals based on many random samples, then we can expect that 95% of the realized intervals would contain the parameter.
  • Since a confidence interval either covers $\theta$ or does not, we cannot say that $\theta$ is in $(l(x),~ u(x))$ with 95% chance.

Steps to construct an interval estimator for $\theta$ using a pivotal quantity

Recall that the goal is to find $l(X_1,\dots,X_n)$ and $u(X_1,\dots,X_n)$ such that

given a confidence coefficient $0<1-\alpha<1$.

Basic idea: use the distribution of a "good" estimator $\widehat{\theta}$ of $\theta$ to decide a "margin" around the point estimate.

The probability that $\hat{\theta}$ is within the distance $\epsilon_n$ of $\theta$ is the same as the probability that $\theta$ is within $\epsilon_n$ distance of $\hat{\theta}$.

Choose $\epsilon_n$ such that $P(|\hat{\theta}-\theta|\leq \epsilon_n) = 1-\alpha$. Then, $P(\hat{\theta} - \epsilon_n \le \theta \le \hat{\theta} +\epsilon_n) = 1-\alpha.$

Example We have a random sample $(X_1,\dots,X_n)$ such that $X_i \sim N(\mu,2^2)$.

$\bar{X}$ is a good estimator of $\mu$. The distribution of $\bar{X}$ = $N(\mu,\frac{4}{n})$.

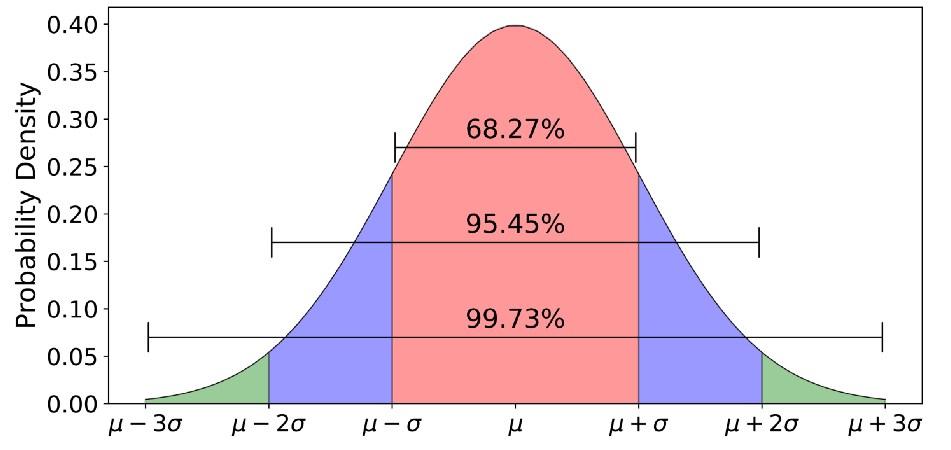
The probability that $\bar{X}$ is within $2\sigma = \frac{4}{\sqrt{n}}$ of $\mu$ $=95.45$%.

Equivalently, the probability that $\mu$ is within $2\sigma = \frac{4}{\sqrt{n}}$ of $\bar{X}$ $=95.45$%.

An interval estimator for $\mu$ : $(\bar{X}-2\frac{2}{\sqrt{n}},\bar{X} +2 \frac{2}{\sqrt{n}})$

• Confidence coefficient: $0.9545$.

Let $(x_1,\dots,x_n)$ be an realization of $(X_1,\dots,X_n)$. The interval estimate for $\mu$ (=95.45% confidence interval) is $(\bar{x}-2 \frac{2}{\sqrt{n}},\bar{x} + 2\frac{2}{\sqrt{n}})$.

Here are general steps:

1. Pick a good estimator $\widehat{\theta}$ of $\theta$.

   • Often, the use of "good" estimators results in good confidence intervals

2. Find or approximate the distribution of an estimator $\widehat{\theta}$ for $\theta$.

   • In particular, we use one of the following three methods:

     • use the exact distribution of an estimator $\widehat{\theta}$
     • use an asymptotic distribution of $\widehat{\theta}$
     • use a numerical method to approximate the distribution of $\widehat{\theta}$

   • Often, we work with the distribution of a function of the estimator $\widehat{\theta}$ and the parameter $\theta$, $f(\widehat{\theta}, \theta)$, whose distribution is known.

     • Such $f(\widehat{\theta},\theta)$ is called as a pivotal quantity ($f$ should not depend on any other unknown parameters than $\theta$).

3. Choose $\epsilon_n$ such that $P(|\hat{\theta}-\theta|\leq \epsilon_n) = 1-\alpha$ based on the distribution of $\hat{\theta}$ or $f(\hat{\theta},\theta)$.

4. An interval estimator with confidence coefficient $1-\alpha$ is $[\hat{\theta}-\epsilon_n, \hat{\theta}+\epsilon_n]$.

Confidence intervals for one mean

Learning objectives

• Know how to compute a $1-\alpha$ confidence interval for $\mu$ when we have

  1. a random sample $(X_1,\dots,X_n)$ from $N(\mu,\sigma^2)$ with known $\sigma^2$
  2. a random sample $(X_1,\dots,X_n)$ from $N(\mu,\sigma^2)$ with unknown $\sigma^2$
  3. a random sample from an unknown distribution but when we have a large sample size

Confidence intervals for one mean

1. Confidence interval for $\mu$ when $X_1, \ldots, X_n\sim N(\mu, \sigma^2)$ with $\sigma^2$ known.

Example: Let $X$ equal the length of life of a 60-watt light bulb marketed by a certain manufacturer. Assume that the distribution of $X$ is $N(\mu, 1296)$. A random sample of $n = 27$ bulbs is tested until they burn out, yielding a sample mean of $\bar{x} = 1478$ hours. Find a 90% and 95% confidence interval for $\mu$.

First, we need to find an interval estimator with the confidence coefficient $1-\alpha$. That is, find $l(X_1,\dots,X_n)$ and $u(X_1,\dots,X_n)$ such that

Then, the realized interval $[l(x_1,\dots,x_n),u(x_1,\dots,x_n)]$ is a $1-\alpha$ confidence interval for $\mu$. How can we find such $l(X_1,\dots,X_n)$ and $u(X_1,\dots,X_n)$?

We follow the four steps to construct an interval estimator:

1. The statistic $\bar{X} = \frac{1}{n}\sum_{i=1}^n X_i$ is a good estimator for $\mu$.

2. Since $X_i \sim N(\mu,\sigma^2)$, by the additive property of the normal distribution, $\bar{X} \sim N(\mu, \frac{\sigma^2}{n})$.

   A pivotal quantity: $f(\bar{X},\mu) = \frac{\bar{X}-\mu} {\sigma/\sqrt{n}} \sim N(0,1)$ (recall that $\sigma^2$ is known).

3. To choose $\epsilon_n$ such that $P(|\bar{X}-\mu|\leq \epsilon_n) = 1-\alpha$, find the number $z_{\alpha/2}$ such that

• The number $z_{\alpha}$ is the 1-$\alpha$ quantile of the standard normal distribution; i.e., the number such that $P(Z>z_{\alpha}) = \alpha$.

  • You can find the number $z_{\alpha}$ in Table V in Appendix B of HTZ.

  • You can use a computer software, such as R, to look up the quantile of the standard normal distribution to find $z_\alpha$. For example, if you want to find $z_{0.025}$ in R, you can run

    qnorm(0.975,mean = 0,sd = 1) #0.975(=1-0.025) quantile of the standard normal dist
    

    to find $z_{0.025} = 1.96$.

• We have $P(|\bar{X}-\mu|\leq z_{\alpha/2} \frac{\sigma}{\sqrt{n}}) = 1-\alpha$.

4. Then, we have $P(|\mu-\bar{X}|\leq z_{\alpha/2} \frac{\sigma}{\sqrt{n}}) = 1-\alpha$.

• An interval estimator for $\mu$ with the confidence coefficient of $\alpha$ = $[\bar{X}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\bar{X} +z_{\alpha/2}\frac{\sigma}{\sqrt{n}}]$ .
• A $1-\alpha$ confidence interval for $\mu$= $[\bar{x}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\bar{x} +z_{\alpha/2}\frac{\sigma}{\sqrt{n}}]$ .

Therefore, 90% and 95% confidence intervals for the average length of life of a 60-watt light bulb are

• 90% confidence interval ($\alpha = 0.1$): $[\bar{x}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\bar{x} +z_{\alpha/2}\frac{\sigma}{\sqrt{n}}] = [1478 - z_{0.05}\frac{36}{\sqrt{27}},1478 + z_{0.05}\frac{36}{\sqrt{27}}]=[1466.6, 1489.4].$
• 95% confidence interval ($\alpha = 0.05$): $[\bar{x}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\bar{x} +z_{\alpha/2}\frac{\sigma}{\sqrt{n}}] = [1478 - z_{0.025}\frac{36}{\sqrt{27}},1478 + z_{0.025}\frac{36}{\sqrt{27}}]=[1464.4, 1491.6].$

Remark In practice, one can never "know" whether the data are from a normal distribution or not. Often, people perform some sorts of normality tests to determine if an observed data set can be well-modeled by a normal distribution. One quick but powerful test is to plot a histogram of the observed data and see whether the shape of histogram resembles a bell-curve.

2. Confidence interval for $\mu$ when $X_1, \ldots, X_n\sim N(\mu, \sigma^2)$ with $\sigma^2$ unknown.

Example: Let $X$ equal the length of life of a 60-watt light bulb marketed by a certain manufacturer. Assume that the distribution of $X$ is normal. A random sample of $n = 27$ bulbs is tested until they burn out, yielding a sample mean of $\bar{x} = 1478$ hours and sample standard deviation of $s = 36$. Construct a 90% and 95% confidence interval for $\mu$.

We construct a confidence interval for $\mu$ when $\sigma^2$ is unknown. Following 4 steps,

1. We use $\bar{X}$ as an estimator of $\mu$.

2. Since each $X_i \sim N(\mu,\sigma^2)$ i.i.d., we have, $\bar{X} \sim N(\mu, \frac{\sigma^2}{n})$.

   We have $\frac{\bar{X}-\mu} {\sigma/\sqrt{n}} \sim N(0,1)$. This is a function of $\bar{X}$, $\mu$ and unknown $\sigma^2$ (not a function of $\bar{X}$ and $\mu$ anymore). We replace the unknown population variance $\sigma^2$ with the sample $S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2$.

   Thus a pivotal quantity $f(\bar{X},\mu) = \frac{\bar{X}-\mu}{S/\sqrt{n}}$.

    

   Lemma: $\frac{\bar{X}-\mu} {S/\sqrt{n}} \sim T(n-1)$, "t-distribution" with a degrees of freedom of $n-1$.

   proof.

   (Theorem 5.5-3 in HTZ) If $Z \sim N(0,1)$, $U \sim \chi^2(d)$, $Z$ and $U$ are independent, then $\frac{Z}{\sqrt{U/d}} \sim T(d)$ .

    

   (Theorem 5.5-2 in HTZ) For $X_1,\dots,X_n \sim N(\mu,\sigma^2)$ i.i.d., we have,

   1. $\bar{X}$ and $\sum_{i=1}^n (X_i - \bar{X})^2$ are independent.
   2. $\sum_{i=1}^n (\frac{X_i - \bar{X}}{\sigma})^2 \sim \chi^2(n-1)$

   In other words, $(n-1)S^2/\sigma^2 \sim \chi^2(n-1)$.

    

   Combining two theorems,

   $$\frac{\bar{X}-\mu} {S/\sqrt{n}} = \frac{(\bar{X}-\mu)/(\sigma/\sqrt{n})} {\sqrt{ \frac{ (n-1)S^2/\sigma^2}{n-1}}} \sim T(n-1)$$

    

3. Find the number $t_{\alpha}(n-1)$ such that

   $$P(-t_{\alpha}(n-1)\leq \frac{\bar{X}-\mu}{S/\sqrt{n}} \leq t_{\alpha}(n-1)) = 1-\alpha$$

   • The number $t_{\alpha}(r)$ is the 1-$\alpha$ quantile of a t distribution with $r$ degrees of freedom; i.e., the number such that $P(T>t_{\alpha}(r)) = \alpha$.

     • You can find the number $t_{\alpha}(r)$ it Table VI in Appendix B of HTZ for some commonly used $\alpha$ values.

     • You can use a computer software, such as R, to look up the value of $t_{\alpha}(r)$. For example, the script

       xxxxxxxxxx
       qt(0.975,df = 10) #0.975(=1-0.025) quantile of the t dist with df = 10
       

       returns $t_{0.025}(10) = 2.23$.

      

    

4. Therefore, $P(|\mu - \bar{X}|\le t_{\alpha}(n-1) \frac{S}{\sqrt{n}}) = 1-\alpha$. In other words,

• An interval estimator for $\mu$ with the confidence coefficient of $\alpha$: $[\bar{X}-t_{\alpha/2}(n-1)\frac{S}{\sqrt{n}},\bar{X} +t_{\alpha/2}(n-1)\frac{S}{\sqrt{n}}]$ .
• A $1-\alpha$ confidence interval for $\mu$= $[\bar{x}-t_{\alpha/2}(n-1)\frac{S}{\sqrt{n}},\bar{x} +t_{\alpha/2}(n-1)\frac{S}{\sqrt{n}}]$ .

Therefore, 90% and 95% confidence intervals for the average length of life of a 60-watt light bulb are

• 90% confidence interval ($\alpha = 0.1$):

  $[\bar{x}-t_{\alpha/2}(n-1)\frac{s}{\sqrt{n}},\bar{x} +t_{\alpha/2}(n-1)\frac{s}{\sqrt{n}}] = [1478 - t_{0.05}(26)\frac{36}{\sqrt{27}},1478 + t_{0.05}(26)\frac{36}{\sqrt{27}}]=[1466.2,1489.8].$

  • In R, qt(0.95,df=26) returns 1.70

• 95% confidence interval ($\alpha = 0.05$):

  $[\bar{x}-t_{\alpha/2}(n-1)\frac{s}{\sqrt{n}},\bar{x} +t_{\alpha/2}(n-1)\frac{s}{\sqrt{n}}] = [1478 - t_{0.025}(26)\frac{36}{\sqrt{27}},1478 + t_{0.025}(26)\frac{36}{\sqrt{27}}]=[1463.8,1492.2].$

  • In R, qt(0.975,df=26) returns 2.01

Remark: we see that $t_{0.05}(26)\geq z_{0.05}$ and $t_{0.025}(26)\geq z_{0.025}$, and thus the length of confidence intervals when $\sigma^2$ is unknown is longer than the confidence intervals when $\sigma^2$ is known. This is because $T(26)$ distribution has a thicker probability tail than the standard normal distribution.

In fact, any $T$ distribution with a finite degrees of freedom has a thicker tail than the standard normal distribution, and as the degrees of freedom increases, the t distribution becomes more similar to a normal distribution. Usually, when the degrees of freedom is over 30, $T$ distribution is quite similar to the standard normal distribution.

3. Confidence interval for $\mu$ with an unknown underlying distribution and large $n$

Example: Let $X$ equal the length of life of a 60-watt light bulb marketed by a certain manufacturer. A random sample of $n = 100$ bulbs is tested until they burn out, yielding a sample mean of $\bar{x} = 1478$ hours. From previous study, it is known that ${\rm Var}(X) = 36$. Construct an approximate 90% and 95% confidence interval for $\mu$.

Since we do not know the distribution of $X_i$, it would be hopeless to find the exact distribution of $\bar{X}$. Luckily, we have a large sample size ($n=100$), and thus we can use the CLT to obtain

Note: even though we know the distribution of $X_i$, it is often hard to obtain the exact distribution of $\bar{X}$. In such cases, we can use this normal approximation instead.

From (1), we have,

Then,

Thus we have,

• an (asymptotically correct) interval estimator for $\mu$ with the confidence coefficient of $\alpha$ = $[\bar{X}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\bar{X} +z_{\alpha/2}\frac{\sigma}{\sqrt{n}}]$ .
• an approximate $1-\alpha$ confidence interval for $\mu$= $[\bar{x}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\bar{x} +z_{\alpha/2}\frac{\sigma}{\sqrt{n}}]$ .

Remark: Here, an "asymptotically correct" interval estimator means the random interval covers the parameter $100(1-\alpha)$% when $n$ is large. In other words, the inequality, $P_\mu(l(X_1,\dots,X_n) \leq \mu \leq u(X_1,\dots,X_n)) \geq 1-\alpha$,

is "correct" when $n$ is large ("asymptotic").

Therefore, approximate 90% and 95% confidence intervals for the average length of life of a 60-watt light bulb are

• 90% confidence interval ($\alpha = 0.1$): $[\bar{x}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\bar{x} +z_{\alpha/2}\frac{\sigma}{\sqrt{n}}] = [1478 - z_{0.05}\frac{36}{\sqrt{100}},1478 + z_{0.05}\frac{36}{\sqrt{100}}]=[1472.1, 1483.9].$
• 95% confidence interval ($\alpha = 0.05$): $[\bar{x}-z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\bar{x} +z_{\alpha/2}\frac{\sigma}{\sqrt{n}}] = [1478 - z_{0.025}\frac{36}{\sqrt{27}},1478 + z_{0.025}\frac{36}{\sqrt{27}}]=[1470.9, 1485.1].$

Suppose the previous knowledge on the population variance $\sigma^2=36$ was unavailable. In such case, we replace the population variance $\sigma^2$ with the sample variance $S^2$ and use the following approximation:

this is due to the fact that $S^2 \approx \sigma^2$ when $n$ is large (more precisely, $S^2$ is a consistent estimator for $\sigma^2$.)

Then, following similar steps as before, we have,

• an (asymptotically correct) interval estimator for $\mu$ with the confidence coefficient of $\alpha$ = $[\bar{X}-z_{\alpha/2}\frac{S}{\sqrt{n}},\bar{X} +z_{\alpha/2}\frac{S}{\sqrt{n}}]$ .
• an approximate $1-\alpha$ confidence interval for $\mu$= $[\bar{x}-z_{\alpha/2}\frac{s}{\sqrt{n}},\bar{x} +z_{\alpha/2}\frac{s}{\sqrt{n}}]$ .

In particular, we can use the same approximate 90% and 95% confidence intervals for the average length of life of a 60-watt light bulb even though the population variance is replaced with the sample variance.

Summary

When we have the observed sample $(x_1,\dots,x_n)$ from a random sample $(X_1,\dots,X_n)$,

Remark: the normal approximation of the distribution of $\bar{X}$ is in general quite good, especially when the distribution of $X_i$ is symmetric, unimodal, and of the continuous type. When the distribution of $X_i$ is highly skewed, a larger sample size is needed for the approximation to be reasonably accurate.

In particular, when the sample size is small and $X_i$ is not normally distributed (especially when heavily skewed), it is preferred to use a numerical method to directly approximate the distribution of $\bar{X}$.

Confidence Intervals for the difference of two means

Learning objectives

• Understand the difference of independent and paired random samples

• Know how to compute a $1-\alpha$ confidence interval for the difference of two population means when we have

  1. two independent random samples $(X_1,\dots,X_{n_X})$, $(Y_1,\dots,Y_{n_Y})$ from $N(\mu_X,\sigma_X^2)$ and $N(\mu_Y,\sigma_Y^2)$ with known $\sigma_X^2$ and $\sigma_Y^2$.
  2. two independent random samples $(X_1,\dots,X_{n_X})$, $(Y_1,\dots,Y_{n_Y})$ from $N(\mu_X,\sigma^2)$ and $N(\mu_Y,\sigma^2)$ with unknown variances (two cases: 1. common variance $\sigma^2=\sigma_X^2=\sigma_Y^2$, 2. different variances $\sigma_X^2 \neq \sigma_Y^2$)
  3. two independent random samples $(X_1,\dots,X_{n_X})$, $(Y_1,\dots,Y_{n_Y})$ from unknown distributions but when we have large sample sizes $n_X$ and $n_Y$.
  4. two paired random samples $(X_1,Y_1),\dots,(X_n,Y_n)$

Two independent random samples vs a paired random sample

Suppose a researcher wants to study whether lack of sleep impacts cognitive performance.

Protocol 1: The researcher recruited 20 participants and divided them into 2 groups. The participants in the first group are allowed to have a normal sleep, but people in the second group are kept awake for 24 hours. Results of cognitive tests are recorded for each patient. Let $X_i$ be the test score result for the $i$ th participant from the first group, and $Y_i$ be the test score result for the $i$ th participant from the second group.

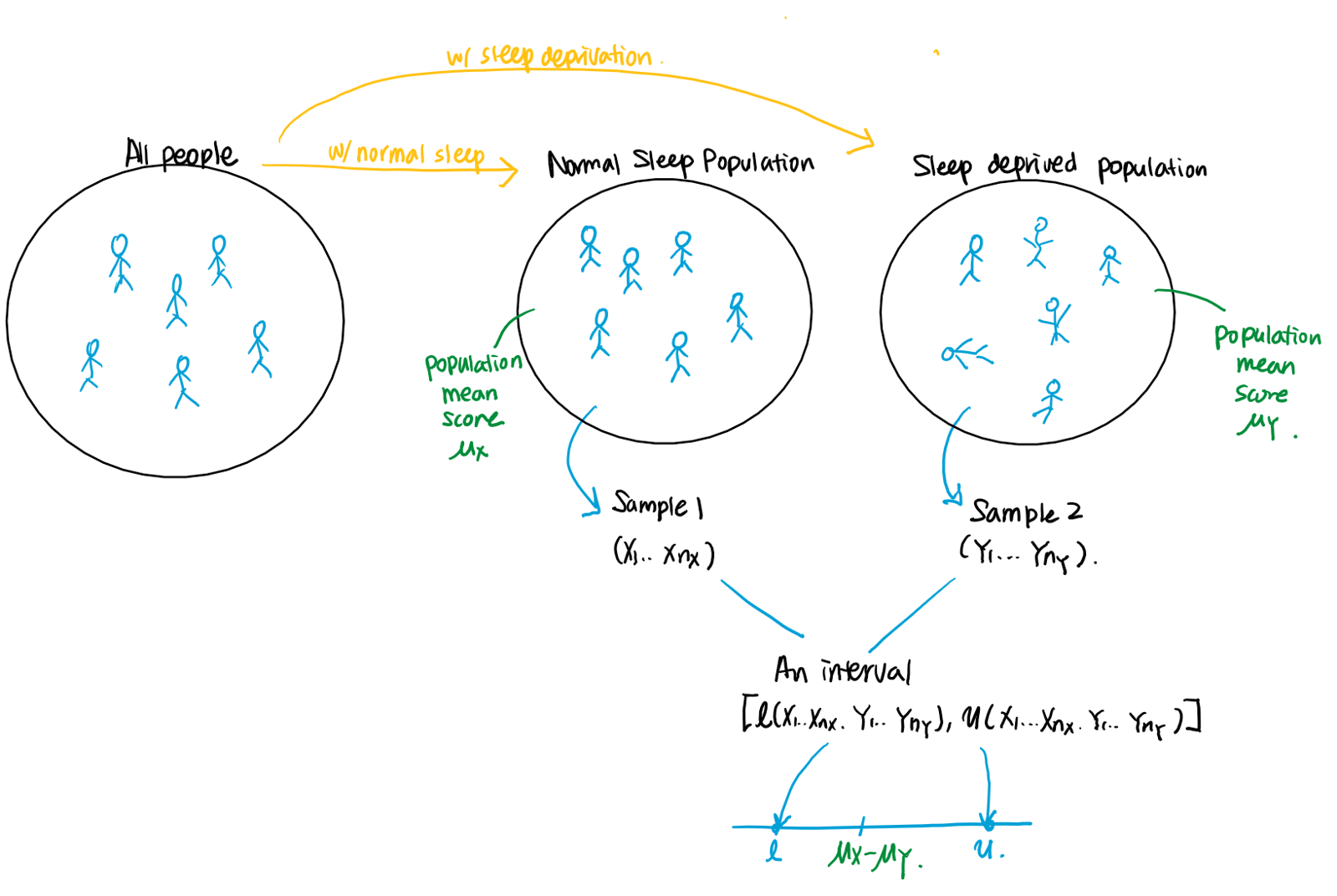
Protocol 2: The researcher recruited 10 participants. Each participant is asked to take the tests twice: one after a normal sleep and the other after being kept awake for 24 hours. Let $X_i$ be the first test score result for the $i$ th participant, and $Y_i$ be the second test score result for the $i$ th participant .

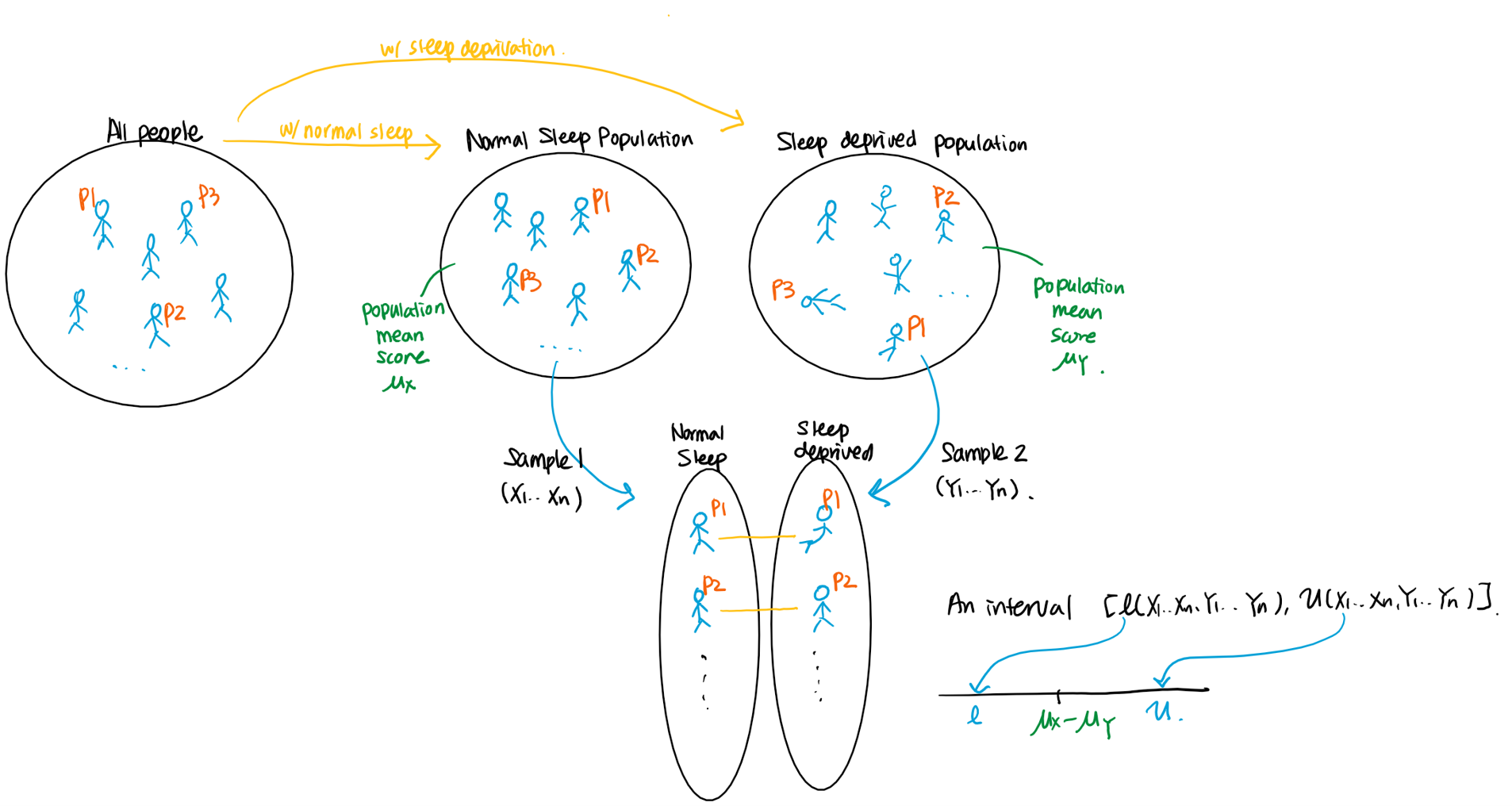
In the first protocol, there is no association between $i$th subject from the first and second group, and therefore $X_i$ and $Y_i$ are independent. On the other hand, in the second protocol, $X_i$ and $Y_i$ are dependent, since the test results are from the same $i$th person. In fact, we have a paired random sample, since each $X_i$ and $Y_i$ should be paired. Therefore,

• Following the first protocol, we would have two independent random samples $(X_1,\dots,X_{10})$ and $(Y_1,\dots,Y_{10})$.
• Following the second protocol, we would have a paired random sample $((X_1,Y_1),\dots,(X_{10},Y_{10}))$.

Confidence intervals for the difference of two means

1. Confidence interval for the difference of the population mean from two independence normal random samples with known variances

Example The researcher followed the first protocol and obtained the following data:

Let $X$ and $Y$ equal the test score of a participant in the first and second group. Based on previous studies, the researcher decided that it is reasonable to assume that the distribution of test scores is normal with the variance of $1$. The researcher wants to form a 95% confidence interval for the difference of test scores between two groups.

Let $\mu_X$ and $\mu_Y$ be unknown population means of group 1 and 2. We need to find an interval estimator with the confidence coefficient $1-\alpha$. That is, find $l(X_1,\dots,X_n)$ and $u(X_1,\dots,X_n)$ such that

We follow the four steps to find an interval estimator:

1. We use an estimator $\bar{X}-\bar{Y}$ for $\mu_X-\mu_Y$.

2. The distribution of $\bar{X}-\bar{Y}$ is $N(\mu_X - \mu_Y, \frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y})$ (using independence of $\bar{X}$ and $\bar{Y}$)

3. The pivotal quantity:

   $$\frac{\bar{X}-\bar{Y}-(\mu_X - \mu_Y)}{\sqrt{ \frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y}}} \sim N(0,1)$$

4. Find $z_{\alpha/2}$ such that

   $$P(-z_{\alpha/2}\leq \frac{\bar{X}-\bar{Y}-(\mu_X - \mu_Y)}{\sqrt{ \frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y}}} \leq z_{\alpha/2}) = 1-\alpha$$

   Therefore, $P(|(\bar{X}-\bar{Y})-(\mu_X - \mu_Y)|\le z_{\alpha/2} \sqrt{\frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y}}) = 1-\alpha$.

5. Rearranging the terms in the event,

   $$P( (\bar{X}-\bar{Y})-z_{\alpha/2}{\sqrt{ \frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y}}} \le \mu_X - \mu_Y\le (\bar{X}-\bar{Y})+z_{\alpha/2}{\sqrt{ \frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y}}}) = 1-\alpha$$

    

   Therefore,

• An interval estimator for $\mu_X-\mu_Y$ with the confidence coefficient of $\alpha$ = $[\bar{X}-\bar{Y}-z_{\alpha/2}\sqrt{ \frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y}},\bar{X}-\bar{Y} +z_{\alpha/2}\sqrt{ \frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y}}]$ .

• A $1-\alpha$ confidence interval for $\mu_X-\mu_Y$:

  $[\bar{x}-\bar{y}-z_{\alpha/2}\sqrt{ \frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y}},\bar{x}-\bar{y} +z_{\alpha/2}\sqrt{ \frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y}}]$

A 95% confidence interval for the difference of test scores between group 1 and group 2 is

$[\bar{x}-\bar{y}-z_{0.025}\sqrt{ \frac{1}{10}+\frac{1}{10}},\bar{x}-\bar{y} +z_{0.025}\sqrt{ \frac{1}{10}+\frac{1}{10}}]= [1.013, 2.767]$

In R,

xxxxxxxxxx
group1 = c(8.4, 9.2, 8.2, 10.6, 9.3, 8.2, 9.5, 9.7, 9.6, 8.7)
group2 = c(8.5, 7.4, 6.4, 4.8, 8.1, 7, 7, 7.9, 7.8, 7.6)
xbar = mean(group1) # compute the sample mean of group 1 data
ybar = mean(group2) # compute the sample mean of group 2 data
margin = qnorm(1-0.025)*sqrt(1/10 + 1/10) 
CI_for_diff = c(xbar-ybar - margin, xbar-ybar + margin) # 95% CI
CI_for_diff
[1] 1.013477 2.766523

2. Confidence interval for the difference of the population mean from two independence normal random samples with unknown variances

Example: Consider the previous sleep study example. However, now the researcher is unsure about whether it is valid to assume that the population variance of each group is $1$. The prior studies indicate that the variances of the scores from each group are likely to be the same. The researcher wants to form a 95% confidence interval for the difference of test scores between two groups.

2-1. Common variance $\sigma^2 = \sigma_X^2 = \sigma_Y^2$

In Step 3, we used

as a pivotal quantity. However, in this setting where $\sigma^2 = \sigma_X^2 = \sigma_Y^2$ is unknown, it is not the function of data and the parameter of interest $\mu_X-\mu_Y$ anymore. We replace $\sigma^2$ with a pooled estimator of the common variance

Lemma:

proof.

Let $Z = \frac{\bar{X}-\bar{Y}-(\mu_X - \mu_Y)}{\sqrt{ \frac{\sigma_X^2}{n_X}+\frac{\sigma_Y^2}{n_Y}}} \sim N(0,1)$, and $U$ such that

$$U = \frac{(n_X+n_Y-2)S_p^2}{\sigma^2} =\sum_{i=1}^{n_X} \frac{(x_i-\bar{x})^2}{\sigma^2} + \sum_{i=1}^{n_Y} \frac{(y_i-\bar{y})^2}{\sigma^2} \sim \chi^2(n_X-1+n_Y-1)$$

By theorem 5.5-3 in HTZ,

$$\frac{\bar{X}-\bar{Y}-(\mu_X - \mu_Y)}{\sqrt{ \frac{S_p^2}{n_X}+\frac{S_p^2}{n_Y}}} = \frac{Z}{\sqrt{U/(n_X+n_Y-2)}}\sim t(n_X+n_Y-2).$$

Following similar steps,

• An interval estimator for $\mu_X-\mu_Y$ with the confidence coefficient of $1-\alpha$ = $[\bar{X}-\bar{Y}-t_{\alpha/2}(n_X+n_Y-2)\sqrt{ \frac{S_p^2}{n_X}+\frac{S_p^2}{n_Y}},\bar{X}-\bar{Y} +t_{\alpha/2}(n_X+n_Y-2)\sqrt{ \frac{S_p^2}{n_X}+\frac{S_p^2}{n_Y}}]$ .

• A $1-\alpha$ confidence interval for $\mu_X-\mu_Y$:

  $[\bar{x}-\bar{y}-t_{\alpha/2}(n_X+n_Y-2)\sqrt{ \frac{s_p^2}{n_X}+\frac{s_p^2}{n_Y}},\bar{x}-\bar{y} +t_{\alpha/2}(n_X+n_Y-2)\sqrt{ \frac{s_p^2}{n_X}+\frac{s_p^2}{n_Y}}]$

Therefore, a 95% confidence interval for the difference of test scores between group 1 and group 2 is

$[\bar{x}-\bar{y}-t_{0.025}(18)\sqrt{ \frac{s_p^2}{10}+\frac{s_p^2}{10}},\bar{x}-\bar{y} +t_{0.025}(18)\sqrt{ \frac{s_p^2}{10}+\frac{s_p^2}{10}}]= [1.023, 2.757]$