Bayesian Estimation

Introduction to Bayesian Estimation

Bayes' Theorem

For two events $A$ and $B$ with positive probability,

Example

Suppose we have one fair coin, and one biased coin which lands Heads with probability $3/4$. One of the coins is picked at random and flipped three times. It lands Heads all three times. Given this information, what is the probability that the coin which is picked is the fair one?

Suppose now we have many coins with different head probabilities. We have prior information that most of the coins are close to being unbiased. How can we incorporate such prior information in our inference for the parameter?

Idea: treat a parameter $\theta$ as a random variable. Make an inference for $\theta$ based on the distribution of $\theta$ given observed data $x_1,\dots,x_n$ (a.k.a. posterior distribution).

• $f(\theta)$ is a pmf/pdf of the prior distribution of $\theta$

• $f(x_1,\dots,x_n|\theta)$ is the conditional pmf/pdf of $x$ given $\theta$. This is the likelihood function of $\theta$.

• $f(\theta|x_1,\dots,x_n)$ is the conditional pmf/pdf of $\theta$ given the observed data $x_1,\dots,x_n$. This is the pmf/pdf of the posterior distribution of $\theta$ given data.

   

By Bayes' theorem,

Choice of a prior distribution

1. Based on prior information (e.g. previous studies)

2. Non-informative prior

3. Conjugate prior

   • a prior distribution that leads to the same distribution for the posterior distribution

A useful trick for posterior distribution computations: note that a pmf/pdf is completely specified by the part of the pmf/pdf which involves an input variable. Thus we first find the form the pdf $p(θ | x_1,\dots,x_n)$, they simply find a "constant" (with respect to $\theta$, which is, of course, actually some function of $x_1,\dots,x_n$) such that the expression integrates to 1.

Example Albert becomes rich after inventing a new type of toothpaste and invests all his money in a random stock. Let $X$ be a random variable that represents the value of the stock today, and let $\theta$ be the long-term mean value of the stock. He found that the value of the stock today was $80. He thinks that this price may be a random realization around the long-term mean $\theta$, and so he assumes that the conditional distribution of $X$ given $\theta$ is $N(\theta, \sigma^2)$ with a known constant $\sigma^2$ (e.g., $\sigma^2=5^2$). Also, based on the past prices of the stock, it seems reasonable to assume that the long-term mean value $\theta$ is a random variable following $N(100, \tau^2)$ with a known constant $\tau^2$ (e.g., $\tau^2=3^2$). Find the posterior distribution of $\theta$.

Point Estimation

Bayesian inferences on the parameters $\theta$ are solely based on the posterior distribution of $\theta$. If we have to make a "best guess" on $\theta$ (point estimation), which value should we choose?

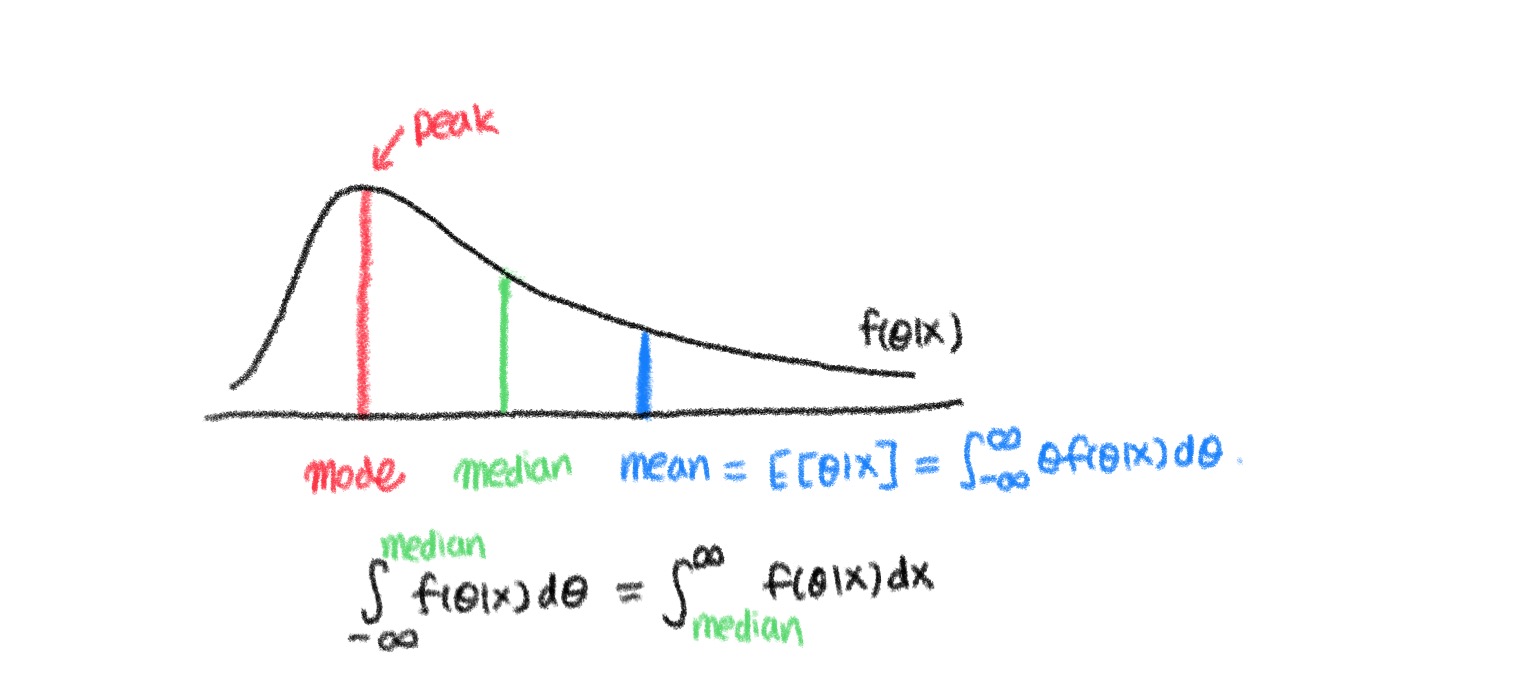
Three most common summary statistics for posterior distributions are

• Posterior mean: expected value of the parameter estimate using the posterior distribution.
• Posterior median: the value which divides the posterior distribution in half
• Posterior mode: the peak of the posterior distribution

Remark: the "best" guess $T$ would clearly depend upon the penalties for various errors created by incorrect guesses.

We use a "loss" function $L(\theta,a)$ to measure the penalty of choosing $a$ as an estimate when $\theta$ is the true value of the parameter.

Examples:

• Squared error loss function: $L(θ, a) = (θ − a)^2$
• Absolute error loss function: $L(θ, a) = |θ − a|$

Definition (Bayes estimator) a Bayes estimator under a loss function $L(\theta,a)$ is an estimator that minimizes the posterior expected value of the loss function.

• The Bayes estimator under the squared error loss $L(\theta,a) =(\theta-a)^2$ is the posterior mean.
• The Bayes estimator under the absolute error loss $L(\theta,a) =(\theta-a)^2$ is the posterior median.

Example: compute the Bayes estimator for the long-term mean $\theta$ in the previous example, when the loss function is the squared error loss.

Bayesian Credible Interval

A Bayesian counterpart to a confidence interval is a Bayesian credible interval.

Definition ($1-\alpha$ credible interval) a $100(1 − α)$% Bayesian credible (or posterior) interval is defined to be any interval $[L,U]$ such that $P(L\le\theta\le U | x_1,\dots,x_n) = 1-\alpha$.

• One common choice for $L$ and $U$ is to let $L= (α/2)$th quantile and $U=(1 − α/2)$th quantile of the posterior distribution.

Remark (Difference with $1-\alpha$ confidence interval)

• The probability that the true parameter is contained within a $1-\alpha$ credible interval is $100(1-\alpha)$%

• $100(1-\alpha)$% of the constructed $1-\alpha$ confidence intervals are expected to contain the true parameter

  • The probability that the true parameter is contained within a $1-\alpha$ confidence interval is either zero or one.

Example: In the example of Albert’s stock investigation, find the 95% posterior interval for the long-term mean $θ$.